[딥러닝] 딥러닝 소개 & 활성함수 & 역전파 계산

- 역치를 넘기는 자극을 신호로 전달하고 반응 -> 뉴런의 아이디어 머신러닝에 도입한 것: 인공신경망(Artificial Neural Network), 신경망 기반으로 학습하는 것이 Deep Learning.

- 초기 신경망 ) XOR 문제 해결하지 못함

  - XOR 문제 해결하는 방법) OR(진리표 0111) & NAND(진리표 1110) gate의 출력을 AND(진리표 0110). 

  - 출력을 또다른 입력으로 -> 다층 퍼셉트론 개념 등장

 

퍼셉트론 (perceptron): 신경망의 최소 단위

 

퍼셉트론, 출처: 위키독스

sum(노드 * 가중치) -> step function -> output

- step function (활성화 함수, activation function): 최종 출력값을 결정하는 함수 - sigmoid, Relu, hyperbolic tangent 등

임계값threshold

- weighted sum -> step function은 한 node 내에서 결정 

 

임계치 입력 퍼셉트론, 출처: 위키독스

 

 

신경망 (Neural Network)

- 다층 퍼셉트론, 퍼셉트론 layer를 늘려 input layer / hidden layer / output layer 로 증가\

함수의 Chain 구조: f(x) = f3(f2(f1(x))) -> 출력이 다시 입력이 되는 ... 합성함수 형태

 

- 순방향 신경망(FFNN: Feed-Forward Neural Network): 입 -> 출력 연산 only

- 순환 신경망(RNN: Recurrent Neural Network): 은닉층 출력값을 출력층으로도 보내는 동시에, 은닉층 출력값이 다시 입력으로 사용

 

- Fully Connected Layer(Dense Layer): 모두 연결된 신경망

 

활성화 함수 Actication Function

은닉층과 출력층 뉴런에서 출력값을 결정하는 함수.

- 은닉 / 출력층에서 인기있게 쓰이는 함수 및 목적에 따라 쓰이는 함수 다름 

- 비선형 함수 (은닉층 돌다보면 값이 너무 커져버림)

 

- Sigmoid: 이진분류(스팸이다/아니다) 출력층에 주로 사용

- Softmax: 다중분류(책이다/논문이다/기사다) 출력층에 주로 사용 (각 값을 %, 확률로 변경해줌)

 

사용 예시

step(거의 미사용), sigmoid(출력층 주로 사용, 출력이 0/1에 가까워지면 기울기 완만해짐) -> 기울기 소실(Vanishing Gradient) 문제 생김 / 기울기 전달율 작아짐

hyperbolic tangent(sigmoid와 문제 비슷하나, 미분했을때 최대값이 1로 sigmoid보다는 큼) / Relu(은닉층에서 주로 사용, 하지만 입력값이 음수면 미분값도 0으로, 해당 뉴런은 그냥 죽어버림 (dying Relu))

Leaky Relu(dying Relu 보완 위함) / Softmax(출력층 다수 사용,다중클래스 분류에서 사용)

 

 

손실함수

- 연속형변수: MSE(Mean Square Error) 사용

- 범주형변수: binary cross entropy / categorical cross entropy 사용

 

Epoch, Batch, Iteration

- Epoch: 모든 데이터를 학습하는 횟수 (전체 데이터셋이 신경망 통과한 횟수)

  - 큰 경우: overfitting 발생 우려

  - 작은 경우: underfitting 발생 우려

- Batch size: 전체 데이터를 작은 그룹으로 나누었을 때 데이터의 양 (데이터 쪼개서 학습할 양)

  - 큰 경우: 학습속도 느리고 메모리 많이 먹음

  - 작은 경우: 가중치 잦은 업데이트로 훈련 불안정해짐

- Iteration(Step): Total / Batch

 

오차 역전파 Back Propagation

- 신경망이 학습하는 방법 (신경망의 가중치를 결정하는 방법, 최적값을 찾아가는 과정)

1) 순전파(forward propagation) 통해 출력값 계산

2) 역전파(back propagation) 통해 1차미분값 계산

3) parameter update

 

출처: 위키독스 https://wikidocs.net/37406

07-05 역전파(BackPropagation) 이해하기

 

1) 순전파 통해 출력값 계산 (활성함수: sigmoid)

 

Step1) 입력 -> 은닉층

 

Step2) 은닉 -> 출력층

 

o1 실제값 0.4, 모델 예측값 0.609, o2 실제값 0.6, 모델 예측값 0.663

MSE 방식으로 전체 오차 Et 계산

target: 실제값, output: 모델 출력값이라고 할 때

 

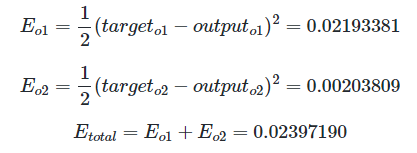
2) 역전파 계산

- 역전파는 출력층 -> 입력층 역순으로 계산하며 가중치를 업데이트 (은닉층 N층일 때, 1단계: 출력 -> 은닉 N층 , 2단계: 은닉 N층 -> 은닉 N-1층)

 

 

 

# 역전파 step1)

1단계에서 업데이트해야하는 가중치는 w5 - w8

w5에 대한 업데이트 위해서는 -> 가중치 행렬 중 w5가 전체 오차에 미치는 영향값 필요 -> 미분의 연쇄법칙 이용해서 알고있는 값 가져오기

좌변이 필요한데 모르니까 : 미분의 연쇄법칙으로 우변처럼 풀어서 계산

 

# 우변 1항에 대한 연산

o1에 대하여 편미분 (나머지는 상수취급)

 

# 우변 2항에 대한 연산

- 시그모이드 함수에 대한 미분 (f(x) * (1 - f(x))

 

# 우변 3항에 대한 연산

-> 순전파를 통해 계산했던 값과 식 잘~변형하면 우변 값 다 가져올 수 있음

 

모든 값 곱해주면 뿅 변화량이 등장

 

 

 

3) 가중치 업데이트

- 경사하강법 (gradient descent) 활용:

업데이트 가중치 = 기존 가중치 - 알파(학습률) * 편미분(전체 오차/업데이트할 가중치) 

- 학습률만큼이 step이 되어 편미분값에 곱해지게 됨 -> 가중치 행렬 중 wn이 변화했을 때, 전체 오차의 변화량 계산하기 위해 편미분 (wn이 변화했을 때 Etotal이 변화하는 값 -> 변화량 찾기 위해 미분)

 

연쇄법칙을 통해 찾은 값과 학습률(0.5가정) 곱해 가중치 업데이트

나머지도 각각 구해 변화량 업데이트

// 이렇게 하면 역전파 1단계 (출력 -> 은닉) 완료

 

# 역전파 step 2: 은닉층 -> 입력층에 대한 역산

비슷한 방식으로 업데이트하면 댐

 

# 결과 확인

역전파 수행 이후의 Etotal이 역전파 전보다 감소하였음